一、范数
定义
范数(norm)是数学中的一种基本概念。在泛函分析中,它定义在赋范线性空间中,并满足一定的条件,即①非负性;②齐次性;③三角不等式。它常常被用来度量某个向量空间(或矩阵)中的每个向量的长度或大小。
范数,是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域,范数是一个函数,是矢量空间内的所有矢量赋予非零的正长度或大小。半范数可以为非零的矢量赋予零长度。
定义范数的矢量空间是赋范矢量空间;同样,定义半范数的矢量空间就是赋半范矢量空间。
Lp norm
公式如下:
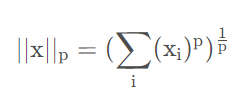
范数即为满足以下三个性质的函数:
- · f(x)= 0 ⇒ x = 0(表达非负性)
- · f(x + y)≤ f(x)+ f(y)(三角不等式)
- · ∀ α ∈ R,f(αx)= | α |f(x)(表达齐次性)
L0 norm
有时候我们会统计向量中非零元素的个数来衡量向量的大小。有些作者将这种函数称为"L0范数",但是这个术语在数学意义上是不对的。向量的非零元素的数目不是范数,因为对向量缩放α 倍不会改变该向量非零元素的数目。因此,L1范数经常作为表示非零元素数目的替代函数。
若用此范数来规则化一个参数矩阵,那就是希望此矩阵中的大部分元素都是零。即L0范数可以使矩阵变得稀疏。
L1 norm
公式如下:
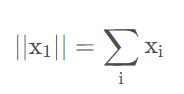
在某些机器学习应用中,区分恰好是零的元素和非零但值很小的元素是很重要的。在这些情况下,我们转而使用在各个位置斜率相同,同时保持简单的数学形式的函数:L1函数。当机器学习问题中零和非零元素之间的差异非常重要时,通常会使用L1函数。每当x 中某个元素从0 增加ϵ,对应的L1函数也会增加ϵ。
L2 norm
公式如下:

L2范数被称为欧几里得范数(Euclidean norm)。它表示从原点出发到向量x 确定的点的欧几里得距离。L2范数在机器学习中出现地十分频繁,经常简化表示为|| x ||,略去了下标2。平方L2范数也经常用来衡量向量的大小,可以简单地通过点积XTX计算。
平方L2范数在数学和计算上都比L2范数本身更方便。例如,平方L2范数对x 中每个元素的导数只取决于对应的元素,而L2范数对每个元素的导数却和整个向量相关。但是在很多情况下,平方L2范数也可能不受欢迎,因为它在原点附近增长得十分缓慢。
L∞ norm
公式如下:
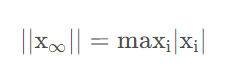
另外一个经常在机器学习中出现的范数是L∞,也被称为最大范数(maxnorm)。这个范数表示向量中具有最大幅值的元素的绝对值。
Frobenius norm
公式如下:
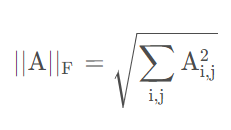
其类似于向量的L2范数。
点积使用范数来表示
公式如下:
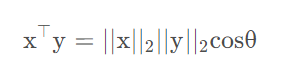
两个向量的点积(dot product)可以用范数来表示。其中θ 表示x和y之间的夹角。
二、梯度
假设函数f : R n → R的输⼊是⼀个n维向量x = [x 1 ,x 2 ,...,x n ] T,输出是标量。函数f(x)有关x的梯度是⼀个由n个偏导数组成的向量:

为表⽰简洁,我们有时⽤▽ f (x)代替▽x f (x)。
假设x是⼀个向量,常⻅的梯度演算包括:
▽x A T x = A,
▽x x T A = A,
▽xx T A x = (A + A T ) x,
▽x|| x || 2 = ▽x x T x = 2 x,
类似地,假设X是⼀个矩阵,那么:
▽x|| X || 2F = 2 X




 川公网安备 51070302110564号
川公网安备 51070302110564号
共有 0 条评论