首先我们需要导入我们需要的包和模块
from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd, nd
import random注:这里导入IPython和matplotlib时需要先在pycharm里安装数据包(参考该分类下的《数据操作》一文)这里我们没有导入%matplotlib inline事实上,这里原文导入的目的是使图像嵌入显示,但是在pycharm中我们有其他做法,我会在后续做出解释。
生成数据集
我们构造⼀个简单的人工训练数据集,设训练数据集样本数为1000,输⼊个数为2。给定随机生成的批量样本特征X ∈ R 1000×2 ,我们使⽤线性回归模型真实权重w = [2,−3.4] T 和偏差b = 4.2,以及⼀个随机噪声项ε来⽣成标签:
y = Xw + b +ε ,
其中噪声项ε服从均值为0、标准差为0.01的正态分布。噪声代表了数据集中无意义的⼲扰。下⾯,让我们生成数据集。
# 定义相关参数
num_input = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
# 构建方程
features = nd.random.normal(scale=1, shape=(num_examples, num_input))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
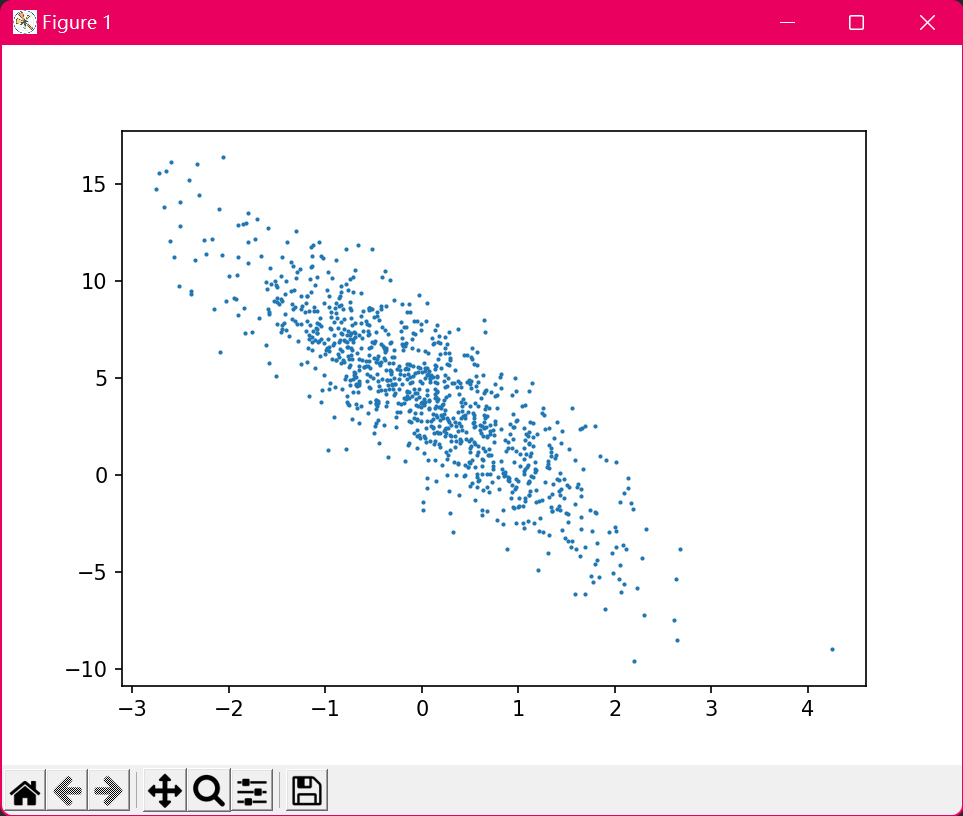
labels += nd.random.normal(scale=0.01, shape=labels.shape)注意,features的每一⾏是一个⻓度为2的向量,而labels的每一⾏是一个⻓度为1的向量(标量)。通过⽣成第⼆个特征features[:, 1]和标签 labels 的散点图,可以更直观地观察两者间的线性关系。
由于所需函数已经在d2lzh中封装好了,所以我们先导入plt模块方便我们使用。
from d2lzh import plt生成散点图:
# 绘制散点图
plt.scatter(features[:, 1].asnumpy(), labels.asnumpy(), 1); # 三个参数分别是x, y轴数据和散点大小
plt.show()注:plt.show()函数便是前面提到的在pycharm中使图像显示的函数。
输出:
读取数据
在训练模型的时候,我们需要遍历数据集并不断读取小批量数据样本。这里我们使用data_iter()函数,它每次返回batch_size(批量⼤小)个随机样本的特征和标签。这个函数也封装在d2lzh包中了,我们可以直接导入使用。
from d2lzh import data_iter让我们读取第⼀个小批量数据样本并打印。每个批量的特征形状为(10, 2),分别对应批量⼤小和输⼊个数;标签形状为批量⼤小。
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
print(X, y)
break输出:
[[-0.6570352 -0.7010761 ]
[ 0.27309823 -0.6894807 ]
[ 0.8488413 0.26954135]
[-0.2243541 -0.00421293]
[-2.513012 1.205448 ]
[ 1.9540555 -1.3049992 ]
[ 0.5613475 -0.61512184]
[ 2.0452461 0.5184493 ]
[ 0.1757906 0.74375474]
[-0.38187912 -1.0473256 ]]
<NDArray 10x2 @cpu(0)>
[ 5.275559 7.0896244 4.9720716 3.7545047 -4.9235134 12.554999
7.412835 6.5239625 2.036555 6.9996033]
<NDArray 10 @cpu(0)>初始化参数模型
我们将权重初始化成均值为0、标准差为0.01的正态随机数,偏差则初始化成0。之后的模型训练中,需要对这些参数求梯度来迭代参数的值,因此我们需要创建它们的梯度。
# 定义w,b
w = nd.random.normal(scale=0.01, shape=(num_input, 1))
b = nd.zeros(shape=(1,))
w.attach_grad()
b.attach_grad()定义模型
我们需要引用函数 linreg(),这个函数也在d2lzh包中封装了,用来实现矢量计算表达式。
from d2lzh import linreg我们通过《查询文档》中的方法查看这个函数的用法:
def linreg(X, w, b):
"""Linear regression."""
return nd.dot(X, w) + b定义损失函数
我们使⽤平⽅损失来定义线性回归的损失函数。在实现中,我们需要把真实值y变形成预测值y_hat的形状,函数返回的结果也将和y_hat的形状相同。squared_loss()函数也是一样,我们可以直接导入。
from d2lzh import squared_loss查看函数用法:
def squared_loss(y_hat, y):
"""Squared loss."""
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2定义优化算法
sgd()函数实现了小批量随机梯度下降算法。它通过不断迭代模型参数来优化损失函数。这⾥⾃动求梯度模块计算得来的梯度是⼀个批量样本的梯度和。我们将它除以批量⼤小来得到平均值。依样导入。
from d2lzh import sgd查看用法:
def sgd(params, lr, batch_size):
"""Mini-batch stochastic gradient descent."""
for param in params:
param[:] = param - lr * param.grad / batch_size在训练中,我们将多次迭代模型参数。在每次迭代中,我们根据当前读取的小批量数据样本(特征X和标签y),通过调⽤反向函数backward计算小批量随机梯度,并调⽤优化算法sgd迭代模型参数。由于我们之前设批量⼤小batch_size为10,每个小批量的损失l的形状为(10, 1)。由于变量l并不是⼀个标量,运⾏l.backward()将对l中元素求和得到新的变量,再求该变量有关模型参数的梯度。(参考《自动求梯度》中对于backward()函数的特别说明)
在⼀个迭代周期(epoch)中,我们将完整遍历⼀遍data_iter函数,并对训练数据集中所有样本都使⽤⼀次(假设样本数能够被批量⼤小整除)。这⾥的迭代周期个数num_epochs和学习率lr都是超参数,分别设3和0.03。在实践中,⼤多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得越⼤模型可能越有效,但是训练时间可能过⻓。而有关学习率对模型的影响,我们在后面再进行详细说明。
# 给定超参学习率和迭代次数
lr = 0.03
num_epochs = 3
# 定义相关函数和样本数量
net = linreg
loss = squared_loss
batch_size = 10
# 迭代
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
with autograd.record():
l = loss(net(X, w, b), y) # 内层函数求模型函数值,外层函数求损失值
l.backward()
sgd([w, b], lr, batch_size) # 迭代函数模型参数
train_l = loss(net(features, w, b), labels) # 使用学习到的参数求本次迭代后的损失值
# 打印每一次迭代后的loss值
print('epoch%d,loss%f' % (epoch + 1, train_l.mean().asnumpy())) # mean()函数求平均值输出:
epoch1,loss0.034981
epoch2,loss0.000125
epoch3,loss0.000049训练完成后,我们可以⽐较学到的参数和⽤来⽣成训练集的真实参数。
# 输出实际参数与学习得到的参数进行比对
print(true_w, w)
print(true_b, b)输出:
[2, -3.4]
[[ 1.9995762]
[-3.399253 ]]
<NDArray 2x1 @cpu(0)>
4.2
[4.200431]
<NDArray 1 @cpu(0)>我们可以发现这些数据非常接近了。
完整代码
下面是完整代码:
from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd, nd
from d2lzh import data_iter, linreg, sgd, squared_loss, plt
import random
"""
构建模型
"""
# 定义相关参数
num_input = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
# 构建方程
features = nd.random.normal(scale=1, shape=(num_examples, num_input))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)
# 绘制散点图
# plt.scatter(features[:, 1].asnumpy(), labels.asnumpy(), 1); # 三个参数分别是x,y轴数据和散点大小
# plt.show()
"""
迭代学习w,b
"""
# 定义w,b
w = nd.random.normal(scale=0.01, shape=(num_input, 1))
b = nd.zeros(shape=(1,))
w.attach_grad()
b.attach_grad()
# 给定超参学习率和迭代次数
lr = 0.03
num_epochs = 3
# 定义相关函数和样本数量
net = linreg
loss = squared_loss
batch_size = 10
# 迭代
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
with autograd.record():
l = loss(net(X, w, b), y) # 内层函数求模型函数值,外层函数求损失值
l.backward()
sgd([w, b], lr, batch_size) # 迭代函数模型参数
train_l = loss(net(features, w, b), labels) # 使用学习到的参数求本次迭代后的损失值
# 打印每一次迭代后的loss值
print('epoch%d,loss%f' % (epoch + 1, train_l.mean().asnumpy())) # mean()函数求平均值
# 输出实际参数与学习得到的参数进行比对
print(true_w, w)
print(true_b, b)小记
在设置batch_size参数时,我们注意到10能整除num_examples参数,如果我们设置此参数为15,使其不能整除num_examples参数时,我们可以发现程序不会报错,但是loss值显著增大。
epoch1,loss0.273798
epoch2,loss0.004623
epoch3,loss0.000130我们减少样本值,单独观察data_iter()函数输出结果:
# 设置num_examples = 50
batch_size = 15
for X, y in data_iter(batch_size, features, labels):
print(X, y, "\n")输出:
[[ 0.5035904 -1.189445 ]
[ 1.5194443 1.9040879 ]
[ 0.25316575 -2.302824 ]
[-1.1081947 0.0787202 ]
[ 0.40093344 0.07440522]
[-0.68106437 -0.1353156 ]
[-1.1877518 -0.15346648]
[-0.22794183 0.20131476]
[ 1.2546344 -0.54877406]
[-2.330265 0.04773738]
[-1.2080863 1.8140212 ]
[ 0.5712682 -2.7579627 ]
[ 0.89039123 -0.27633253]
[-1.5734432 -0.14007866]
[-0.36147118 -1.0910612 ]]
<NDArray 15x2 @cpu(0)>
[ 9.252751 0.7669491 12.527864 1.7205405 4.7728887 3.2663863
2.3645537 3.0580494 8.584421 -0.63497555 -4.3789067 14.714223
6.922372 1.5120044 7.191746 ]
<NDArray 15 @cpu(0)>
[[ 0.6850326 1.174712 ]
[ 1.07628 -0.6141325 ]
[ 0.37723133 0.41016456]
[-1.7305615 0.6770596 ]
[ 1.6881202 -0.6523198 ]
[ 0.13385749 -0.7531863 ]
[-0.9185634 -0.74571437]
[ 1.9670967 -1.3998121 ]
[-0.85567254 -0.8239901 ]
[ 1.8307649 -1.1468065 ]
[ 1.9417537 0.7879354 ]
[ 1.1630785 0.4838046 ]
[ 1.3677438 1.0384175 ]
[-1.1688148 1.558071 ]
[-0.5459446 -2.3556297 ]]
<NDArray 15x2 @cpu(0)>
[ 1.5795556 8.431999 3.5818381 -1.5505313 9.807897 7.0181017
4.8893595 12.903617 5.2878633 11.741857 5.41447 4.873973
3.3972235 -3.4398537 11.105512 ]
<NDArray 15 @cpu(0)>
[[ 1.2446454 0.57413304]
[-0.26470134 -0.63217986]
[-0.55021375 -1.5918757 ]
[ 0.7544733 -0.9463356 ]
[-0.11104874 1.9420102 ]
[-0.8062886 -1.200044 ]
[ 0.15606561 -0.56803983]
[-0.5916499 0.85860497]
[ 0.54144025 2.6785064 ]
[ 0.29670075 1.3111951 ]
[ 0.29956347 0.15302546]
[ 0.5187018 0.15364595]
[ 0.43909982 -0.46219134]
[-1.3549325 -0.957484 ]
[ 0.05383794 -2.5074806 ]]
<NDArray 15x2 @cpu(0)>
[ 4.7498116 5.8368483 8.51521 8.9278 -2.6085293 6.67851
6.46503 0.09388295 -3.8319643 0.3358111 4.28996 4.7179956
6.6548243 4.73344 12.825904 ]
<NDArray 15 @cpu(0)>
[[ 0.24606876 -1.053679 ]
[ 1.0113305 -0.42647716]
[-2.5028148 -0.28589353]
[ 0.3500547 0.5360521 ]
[-1.522743 -2.515245 ]]
<NDArray 5x2 @cpu(0)>
[8.2822075 7.6527014 0.1567788 3.0955064 9.697303 ]
<NDArray 5 @cpu(0)> 我们看见最后一组输出仅有5组,所以我们可以看出,data_iter()函数依然会输出,当输出组数不满足预定值时会将剩余结果全部输出,此时,最后一组样本数量过少就会导致误差增大,导致最终loss值增大,影响模型学习结果。所以我们在设置batch_size参数时也要注意这一问题。



 川公网安备 51070302110564号
川公网安备 51070302110564号
共有 0 条评论