生成数据集

和线性回归（1）中的步骤完全一致，可以参考前文同一小结。

读取数据

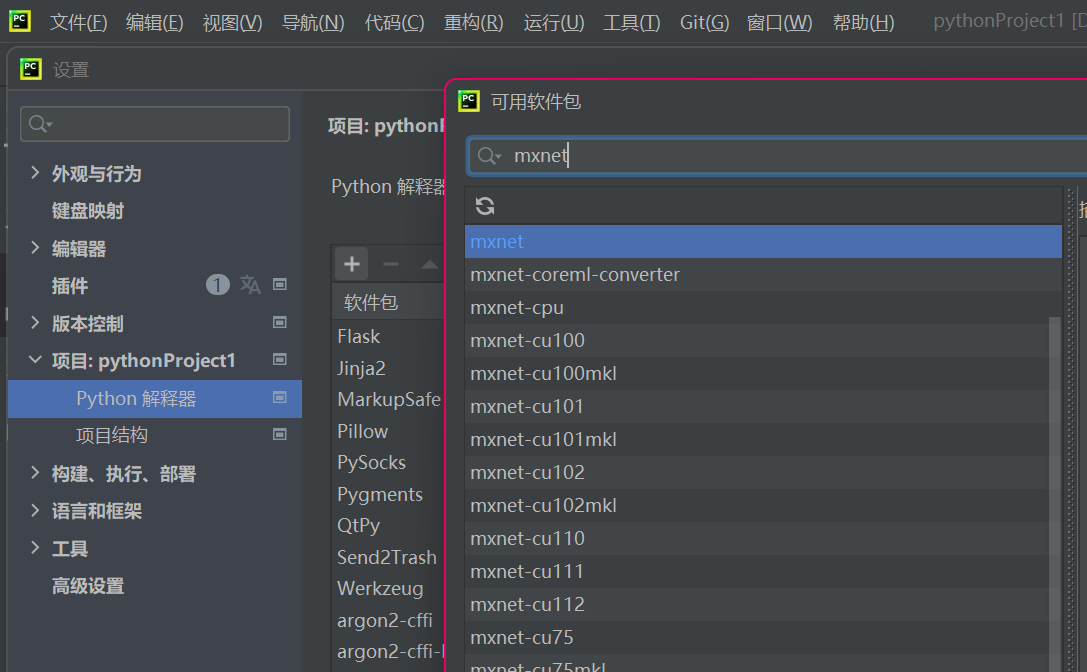
Gluon提供了data包来读取数据。由于data常⽤作变量名，我们将导⼊的data模块⽤添加了Gluon⾸字⺟的假名gdata代替。在每一次迭代中，我们将随机读取包含10个数据样本的小批量。

from mxnet.gluon import data as gdata

batch_size = 10

dataset = gdata.ArrayDataset(features, labels)  # 把数据特征features和标签labels结合
data_iter = gdata.DataLoader(dataset, batch_size, shuffle=True)  # 随机读取小批量

定义模型

Gluon提供了大量预定义的层，这使我们只需关注使⽤哪些层来构造模型。首先，导入nn模块。

from mxnet.gluon import nn

实际上，“nn”是neural networks（神经网络）的缩写。顾名思义，该模块定义了大量神经网络的层。我们先定义一个模型变量net，它是一个Sequential实例。在Gluon中，Sequential实例可以看作是一个串联各个层的容器。在构造模型时，我们在该容器中依次添加层。当给定输⼊数据时，容器中的每一层将依次计算并将输出作为下一层的输入。

net = nn.Sequential()

作为一个单层神经网络，线性回归输出层中的神经元和输⼊层中各个输⼊完全连接。因此，线性回归的输出层又叫全连接层。在Gluon中，全连接层是一个Dense实例。我们定义该层输出个数为1。

net.add(nn.Dense(1))

注：在Gluon中我们无须指定每一层输⼊的形状，例如线性回归的输⼊个数。当模型得到数据时，例如后⾯执⾏net(X)时，模型将自动推断出每一层的输⼊个数。

初始化模型参数

在使用net前，我们需要初始化模型参数，如线性回归模型中的权重和偏差。我们从MXNet导⼊init模块。

from mxnet import init

该模块提供了模型参数初始化的各种方法。这⾥的init是initializer的缩写形式。我们通过init.Normal(sigma=0.01)指定权重参数每个元素将在初始化时随机采样于均值为0、标准差为0.01的正态分布。偏差参数默认会初始化为零。

net.initialize(init.Normal(sigma=0.01))

定义损失函数

在Gluon中，loss模块定义了各种损失函数。我们用假名gloss代替导⼊的loss模块，并直接使用它提供的平方损失作为模型的损失函数。

from mxnet.gluon import loss as gloss

loss = gloss.L2Loss()   # 平方损失也称L2范数损失

定义优化算法

在导⼊Gluon后，我们创建一个Trainer实例，并指定学习率为0.03的小批量随机梯度下降（sgd）为优化算法。该优化算法将⽤来迭代net实例所有通过add函数嵌套的层所包含的全部参数。这些参数可以通过collect_params函数获取。

from mxnet import gluon

trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.03})

训练模型

在使⽤Gluon训练模型时，我们通过调用Trainer实例的step函数来迭代模型参数。按照小批量随机梯度下降的定义，我们在step函数中指明批量大小，从而对批量中样本梯度求平均。

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        with autograd.record():
            l = loss(net(X), y)
        l.backward()
        trainer.step(batch_size)
    l = loss(net(features), labels)
    print('loss：%f' % l.mean().asnumpy())

输出：

0.034983
0.000126
0.000048

我们分别⽐较学到的模型参数和真实的模型参数。我们从net获得需要的层，并访问其权重（weight）和偏差（bias）。

dense = net[0]  
print(true_w, dense.weight.data())
print(true_b, dense.bias.data())

输出：

[2, -3.4] 
[[ 1.999671  -3.3996086]]
<NDArray 1x2 @cpu(0)>
4.2 
[4.1998878]
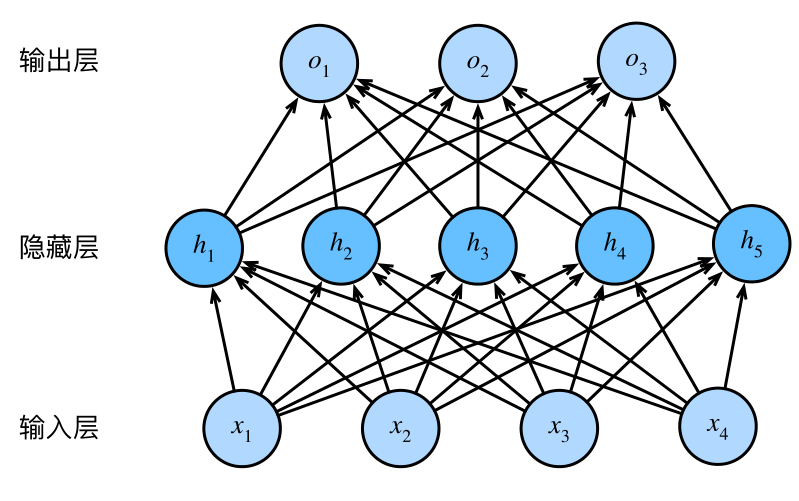
<NDArray 1 @cpu(0)>

net[0]：在《线性回归基础》一文中我们分析线性回归神经网络图时我们提到，由于输⼊层并不涉及计算，按照惯例，这样的神经⽹络的层数为1，所以这里我们读取的数据储存在第一层，即net[0]。

"weight"，"bias"： 我们追根溯源，发现构建神经网络时的Dense函数是我们需要的，我们查看此函数的用法：

    def __init__(self, units, activation=None, use_bias=True, flatten=True,
                 dtype='float32', weight_initializer=None, bias_initializer='zeros',
                 in_units=0, **kwargs):
        super(Dense, self).__init__(**kwargs)
        self._flatten = flatten
        with self.name_scope():
            self._units = units
            self._in_units = in_units
            self.weight = self.params.get('weight', shape=(units, in_units),
                                          init=weight_initializer, dtype=dtype,
                                          allow_deferred_init=True)
            if use_bias:
                self.bias = self.params.get('bias', shape=(units,),
                                            init=bias_initializer, dtype=dtype,
                                            allow_deferred_init=True)
            else:
                self.bias = None
            if activation is not None:
                self.act = Activation(activation, prefix=activation+'_')
            else:
                self.act = None

我们从中可以看出，我们要找的参数就是weight和bias，我们输出即可。

完整代码

from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd, nd, init, gluon
from d2lzh import linreg, sgd, squared_loss, plt
from mxnet.gluon import data as gdata
from mxnet.gluon import loss as gloss
from mxnet.gluon import nn
import random

num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2

features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)

batch_size = 10

dataset = gdata.ArrayDataset(features, labels)  # 把数据特征features和标签labels结合
data_iter = gdata.DataLoader(dataset, batch_size, shuffle=True)  # 随机读取小批量

net = nn.Sequential()
net.add(nn.Dense(1))

net.initialize(init.Normal(sigma=0.01))
loss = gloss.L2Loss()   # 平方损失也称L2范数损失
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.03})

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        with autograd.record():
            l = loss(net(X), y)
        l.backward()
        trainer.step(batch_size)
    l = loss(net(features), labels)
    print('loss：%f' % l.mean().asnumpy())

dense = net[0]
print(true_w, dense.weight.data())
print(true_b, dense.bias.data())