隐藏层

多层感知机在单层神经⽹络的基础上引⼊了⼀到多个隐藏层（hidden layer）。隐藏层位于输⼊层和输出层之间。如图：

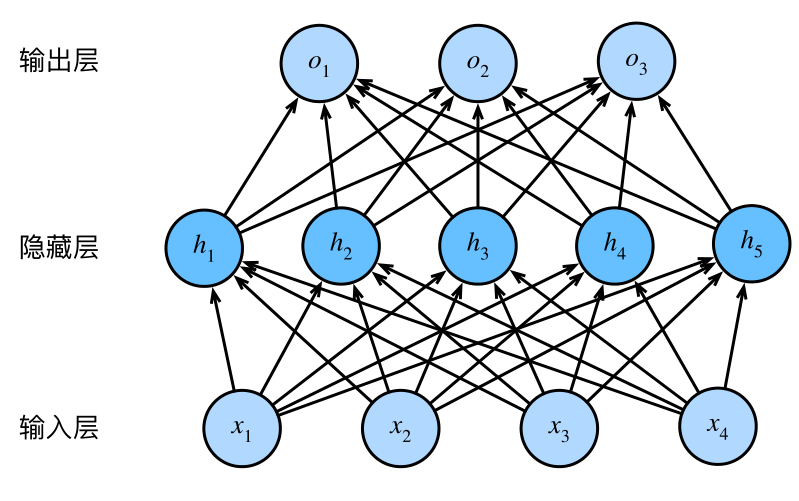
隐藏层中的神经元和输⼊层中各个输⼊完全连接，输出层中的神经元和隐藏层中的各个神经元也完全连接。因此，多层感知机中的隐藏层和输出层都是全连接层。

激活函数

ReLU（rectified linear unit）函数提供了⼀个很简单的⾮线性变换。给定元素x，该函数定义为

ReLU(x) = max(x,0).

可以看出，ReLU函数只保留正数元素，并将负数元素清零。

import d2lzh as d2l
from mxnet import autograd, nd


def xyplot(x_vals, y_vals, name):
    d2l.set_figsize(figsize=(5, 2.5))
    d2l.plt.plot(x_vals.asnumpy(), y_vals.asnumpy())
    d2l.plt.xlabel('x')
    d2l.plt.ylabel(name + '(x)')
    d2l.plt.show()  # 展示图象


x = nd.arange(-8.0, 8.0, 0.1)
x.attach_grad()
with autograd.record():
    y = x.relu()
y.backward()

xyplot(x, y, 'relu')  # relu函数图像
xyplot(x, x.grad, 'grad of relu')  # relu函数导函数图像

输出：

relu函数图像

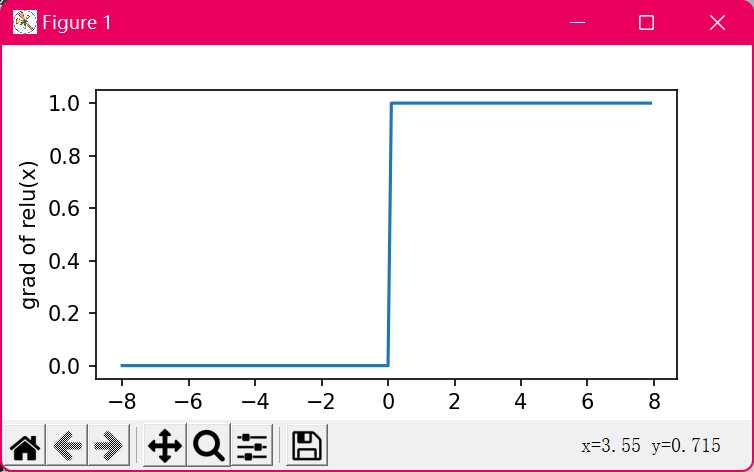
relu函数导函数图像

显然，当输⼊为负数时，ReLU函数的导数为0；当输⼊为正数时，ReLU函数的导数为1。尽管输⼊为0时ReLU函数不可导，但是我们可以取此处的导数为0。

sigmoid函数

sigmoid函数可以将元素的值变换到0和1之间：

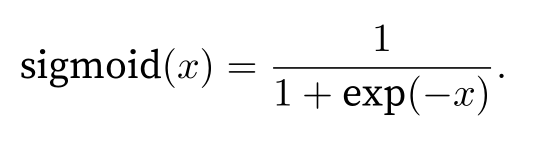
import d2lzh as d2l
from mxnet import autograd, nd


def xyplot(x_vals, y_vals, name):
    d2l.set_figsize(figsize=(5, 2.5))
    d2l.plt.plot(x_vals.asnumpy(), y_vals.asnumpy())
    d2l.plt.xlabel('x')
    d2l.plt.ylabel(name + '(x)')
    d2l.plt.show()  # 展示图象


x = nd.arange(-8.0, 8.0, 0.1)
x.attach_grad()
with autograd.record():
    y = x.sigmoid()
y.backward()

xyplot(x, y, 'sigmoid')  # sigmoid函数图像
xyplot(x, x.grad, 'grad of sigmoid')  # sigmoid函数导函数图像

输出：

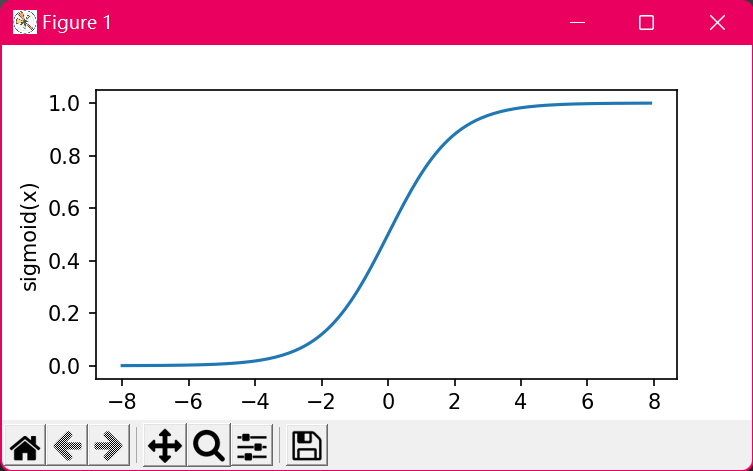
sigmoid函数图像

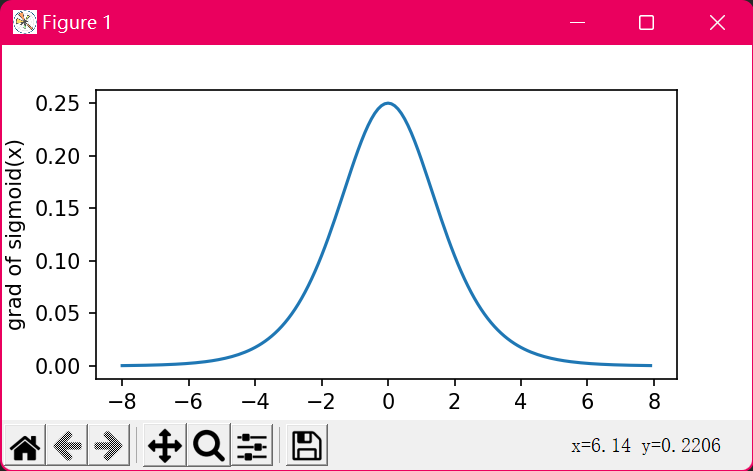
sigmoid函数导函数图像

当输⼊接近0时，sigmoid函数接近线性变换。当输⼊为0时，sigmoid函数的导数达到最⼤值0.25；当输⼊越偏离0时，sigmoid函数的导数越接近0。

tanh函数

tanh（双曲正切）函数可以将元素的值变换到-1和1之间：

import d2lzh as d2l
from mxnet import autograd, nd


def xyplot(x_vals, y_vals, name):
    d2l.set_figsize(figsize=(5, 2.5))
    d2l.plt.plot(x_vals.asnumpy(), y_vals.asnumpy())
    d2l.plt.xlabel('x')
    d2l.plt.ylabel(name + '(x)')
    d2l.plt.show()  # 展示图象


x = nd.arange(-8.0, 8.0, 0.1)
x.attach_grad()
with autograd.record():
    y = x.tanh()
y.backward()

xyplot(x, y, 'tanh')  # tanh函数图像
xyplot(x, x.grad, 'grad of tanh')  # tanh函数导函数图像

输出：

tanh函数图像

tanh函数导函数图像

当输⼊接近0时，tanh函数接近线性变换。tanh函数在坐标系的原点上对称。当输⼊为0时，tanh函数的导数达到最⼤值1；当输⼊越偏离0时，tanh函数的导数越接近0。

多层感知机

多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络，且每个隐藏层的输出通过激活函数进⾏变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿⽤本节之前定义的符号，多层感知机按以下方式计算输出：

H = φ(XW _h + b _h )，

O = HW _o + b _o ，

其中φ表示激活函数。在分类问题中，我们可以对输出O做softmax运算，并使⽤softmax回归中的交叉熵损失函数。在回归问题中，我们将输出层的输出个数设为1，并将输出O直接提供给线性回归中使⽤的平方损失函数。