线性回归输出是一个连续值,因此适⽤于回归问题。
基本要素
模型
设房屋的⾯积为x 1 ,房龄为x 2 ,售出价格为y。我们需要建⽴基于输⼊x 1 和x 2来计算输出y的表达式,也就是模型(model)。顾名思义,线性回归假设输出与各个输⼊之间是线性关系:
yˆ = x 1 w 1+x 2 w 2 +b,
其中w 1和w 2 是权重(weight),b是偏差(bias),且均为标量。它们是线性回归模型的参数(pa-rameter)。模型输出yˆ 是线性回归对真实价格y的预测或估计。我们通常允许它们之间有⼀定误差。
模型训练
接下来我们需要通过数据来寻找特定的模型参数值,使模型在数据上的误差尽可能小。这个过程叫作模型训练(model training)。下⾯我们介绍模型训练所涉及的3个要素。
训练数据
我们通常收集⼀系列的真实数据,例如多栋房屋的真实售出价格和它们对应的⾯积和房龄。我们希望在这个数据上⾯寻找模型参数来使模型的预测价格与真实价格的误差最小。在机器学习术语⾥,该数据集被称为训练数据集(training data set)或训练集(training set),⼀栋房屋被称为⼀个样本(sample),其真实售出价格叫作标签(label),⽤来预测标签的两个因素叫作特征(feature)。特征⽤来表征样本的特点。
假设我们采集的样本数为n,索引为i的样本的特征为x 1(i)和x 2(i),标签为y (i) 。对于索引为i的房屋,线性回归模型的房屋价格预测表达式为:
y ^(i)= x 1(i) w 1+x 2(i) w 2 +b,
损失函数
在模型训练中,我们需要衡量价格预测值与真实值之间的误差。通常我们会选取⼀个⾮负数作为误差,且数值越小表⽰误差越小。⼀个常⽤的选择是平⽅函数。它在评估索引为i的样本误差的表达式为:

其中常数1/2使对平⽅项求导后的常数系数为1,这样在形式上稍微简单⼀些。显然,误差越小表⽰预测价格与真实价格越相近,且当⼆者相等时误差为0。给定训练数据集,这个误差只与模型参数相关,因此我们将它记为以模型参数为参数的函数。在机器学习⾥,将衡量误差的函数称为损失函数(loss function)。这⾥使⽤的平⽅误差函数也称为平⽅损失(square loss)。通常,我们⽤训练数据集中所有样本误差的平均来衡量模型预测的质量,即:

在模型训绿中,我们希望找出一组模型参数,记为w 1*,w 2*和b *,来使训样本平均损失最小:

优化算法
当模型和损失函数形式较为简单时,上⾯的误差最小化问题的解可以直接⽤公式表达出来。这类解叫作解析解(analytical solution)。本节使⽤的线性回归和平⽅误差刚好属于这个范畴。然而,⼤多数深度学习模型并没有解析解,只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解(numerical solution)。
在求数值解的优化算法中,小批量随机梯度下降(mini-batch stochastic gradient descent)在深度学习中被⼴泛使⽤。它的算法很简单:先选取⼀组模型参数的初始值,如随机选取;接下来对参数进⾏多次迭代,使每次迭代都可能降低损失函数的值。在每次迭代中,先随机均匀采样⼀个由固定数⽬训练数据样本所组成的小批量(mini-batch)β,然后求小批量中数据样本的平均损失有关模型参数的导数(梯度),最后⽤此结果与预先设定的⼀个正数的乘积作为模型参数在本次迭代的减小量。
在训练本节讨论的线性回归模型的过程中,模型的每个参数将作如下迭代:

在上式中,|β|代表每个小批量中的样本个数(批量⼤小,batch size),η称作学习率(learningrate)并取正数。需要强调的是,这⾥的批量⼤小和学习率的值是⼈为设定的,并不是通过模型训练学出的,因此叫作超参数(hyperparameter)。我们通常所说的“调参”指的正是调节超参数,例如通过反复试错来找到超参数合适的值。在少数情况下,超参数也可以通过模型训练学出。对此类情况不做讨论。
模型预测
模型训练完成后,我们将模型参数w 1,w 2和b *在优化算法停⽌时的值分别记作 w 1ˆ , w 2ˆ , bˆ。注意,这⾥我们得到的并不⼀定是最小化损失函数的最优解w 1*,w 2*和b * ,而是对最优解的⼀个近似。然后,我们就可以使⽤学出的线性回归模型x 1 w 1ˆ+x 2 w 2 ˆ+bˆ,来估算训练数据集以外任意一栋⾯积(平⽅⽶)为x 1 、房龄(年)为x 2 的房屋的价格了。这⾥的估算也叫作模型预测、模型推断或模型测试。
线性回归的表示方法
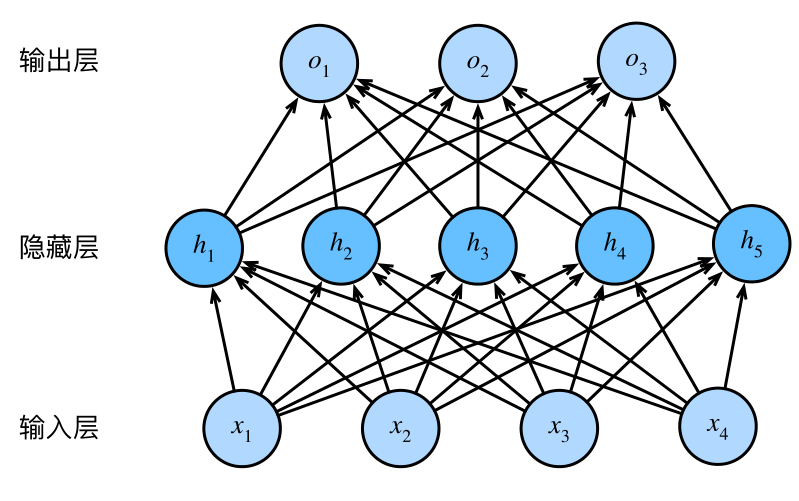
在深度学习中,我们可以使用神经网络图直观地表现模型结构。为了更清晰地展⽰线性回归作为神经网络的结构,下图使用神经网络图表⽰本节中介绍的线性回归模型。神经网络图隐去了模型参数权重和偏差。

在上图的神经⽹络中,输⼊分别为x 1 和x 2 ,因此输⼊层的输⼊个数为2。输⼊个数也叫特征数或特征向量维度。上图中⽹络的输出为o,输出层的输出个数为1。需要注意的是,我们直接将上图中神经⽹络的输出o作为线性回归的输出,即y ˆ = o。由于输⼊层并不涉及计算,按照惯例,上图所⽰的神经⽹络的层数为1。所以,线性回归是⼀个单层神经⽹络。输出层中负责计算o的单元⼜叫神经元。在线性回归中,o的计算依赖于x 1 和x 2 。也就是说,输出层中的神经元和输⼊层中各个输⼊完全连接。因此,这⾥的输出层⼜叫全连接层(fully-connected layer)或稠密层(dense layer)。
⽮量计算表达式
在模型训练或预测时,我们常常会同时处理多个数据样本并⽤到⽮量计算。向量相加的⼀种⽅法是,将这两个向量按元素逐⼀做标量加法。向量相加的另⼀种⽅法是,将这两个向量直接做⽮量加法。考虑计算效率,我们尽可能采⽤⽮量计算。
如果我们对训练数据集⾥的3个房屋样本(索引分别为1、2和3)逐⼀预测价格,将得到:

现在,我们将上⾯3个等式转化成⽮量计算。设:

对3个房屋样本预测价格的⽮量计算表达式为yˆ = Xw + b。
广义上讲,当数据样本数为n,特征数为d时,线性回归的⽮量计算表达式为:
yˆ = Xw + b
其中模型输出y ˆ ∈ R n×1 ,批量数据样本特征X ∈ R n×d ,权重w ∈ R d×1 ,偏差b ∈ R。相应地,批量数据样本标签y ∈ R n×1 。设模型参数θ = [w 1 ,w 2 ,b] T ,我们可以重写损失函数为:

小批量随机梯度下降的迭代步骤将相应地改写为:

其中梯度是损失有关3个为标量的模型参数的偏导数组成的向量:




 川公网安备 51070302110564号
川公网安备 51070302110564号
hututu博主
😎